6.2 General Case with Standard Normal Distributions

In probability theory and statistics, a collection of random variables is independent and identically distributed (iid) if each random variable has the same probability distribution as the others and all are mutually independent. Following, we are going to perform a Monte Carlo simulation to check two main iid properties:

• The expected value of absolute difference is: \(E(|X-Y|)=\frac{2}{\sqrt{\pi}}\)
• The variance of absolute difference is: \(V(|X-Y|) = 2- \frac{4}{\pi}\)

We generate a large number of random samples of size 2 from a standard normal distribution, then compute the replicate pairs’ differences, and then the mean of those differences:

set.seed(2021)
n = 10000
g = numeric(n)

for (i in 1:n) {
  x = rnorm(2)
  g[i] = abs(x[1] - x[2])
}

estMean = mean(g)
expectedValue = 2/sqrt(pi)
diffMeanExpectation = abs(estMean-expectedValue)

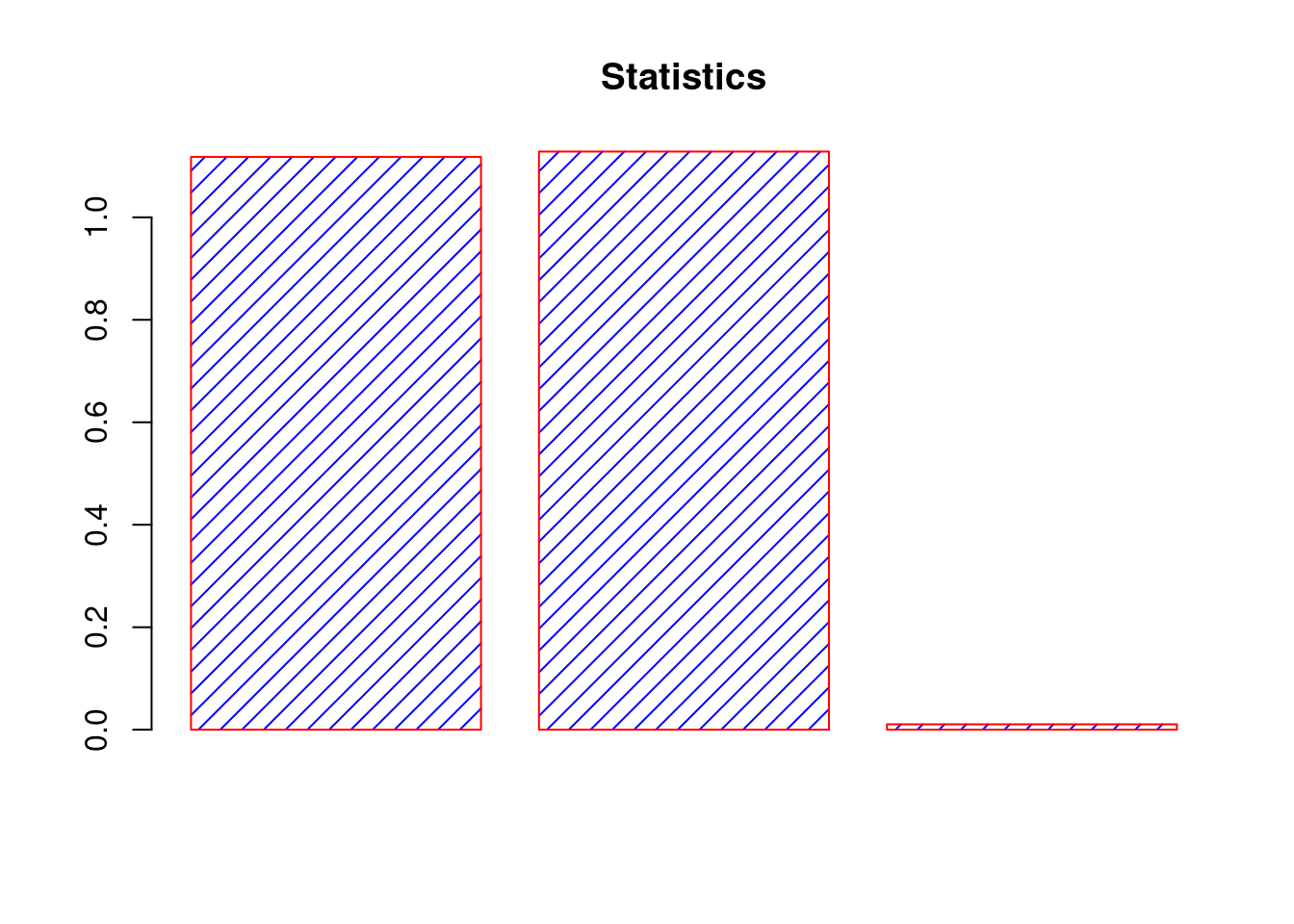
c("Estimated Mean" = estMean, "Expected Value" = expectedValue, "Difference" = diffMeanExpectation)

## Estimated Mean Expected Value     Difference 
##     1.11782094     1.12837917     0.01055823

Next, we can see a plot that represents the results.

library(ggplot2)

dataPlot = c(estMean, expectedValue, diffMeanExpectation)
barplot(dataPlot, main = "Statistics", border="red", col="blue", density=12)