6.1 Monte Carlo for estimation
Let’s begin with simply estimating a probability. Sometimes this is referred to as computing an expectation of a random variable. If you have a random variable \(X\) with a density function \(f_X(x)\) and we want to compute the expectation of a function \(g(x)\) which models the probability of \(f_X(x)\), (or the area under the curve of \(f_X(x)\)), then \(g(x)\) can be expressed as the integral of \(f_X(x)\).
6.1.1 Sam and Annie from ‘Sleepless in Seattle’
We can take a look to the Sleepless in Seattle video to understand the problem. It is a 1993 American romantic comedy.
Now, let \(A\) and \(S\) represent Sam’s and Annie’s arrival times at the Empire State Building, where we measure the arrival time as the number of hours after noon. We assume:
- \(A\) and \(S\) are independent and uniformly distributed
- Annie arrives somewhere between 10:30 and midnight
- Sam arrives somewhere between 10:00 and 11:30PM.
Our Questions are:
- What is the probability that Annie arrives before Sam?
- What is expected difference in arrival times?
We start simulating a large number of values from distribution of \((A,S)\) say, 1000, where \(A\) and \(S\) are independent:
set.seed(2021)
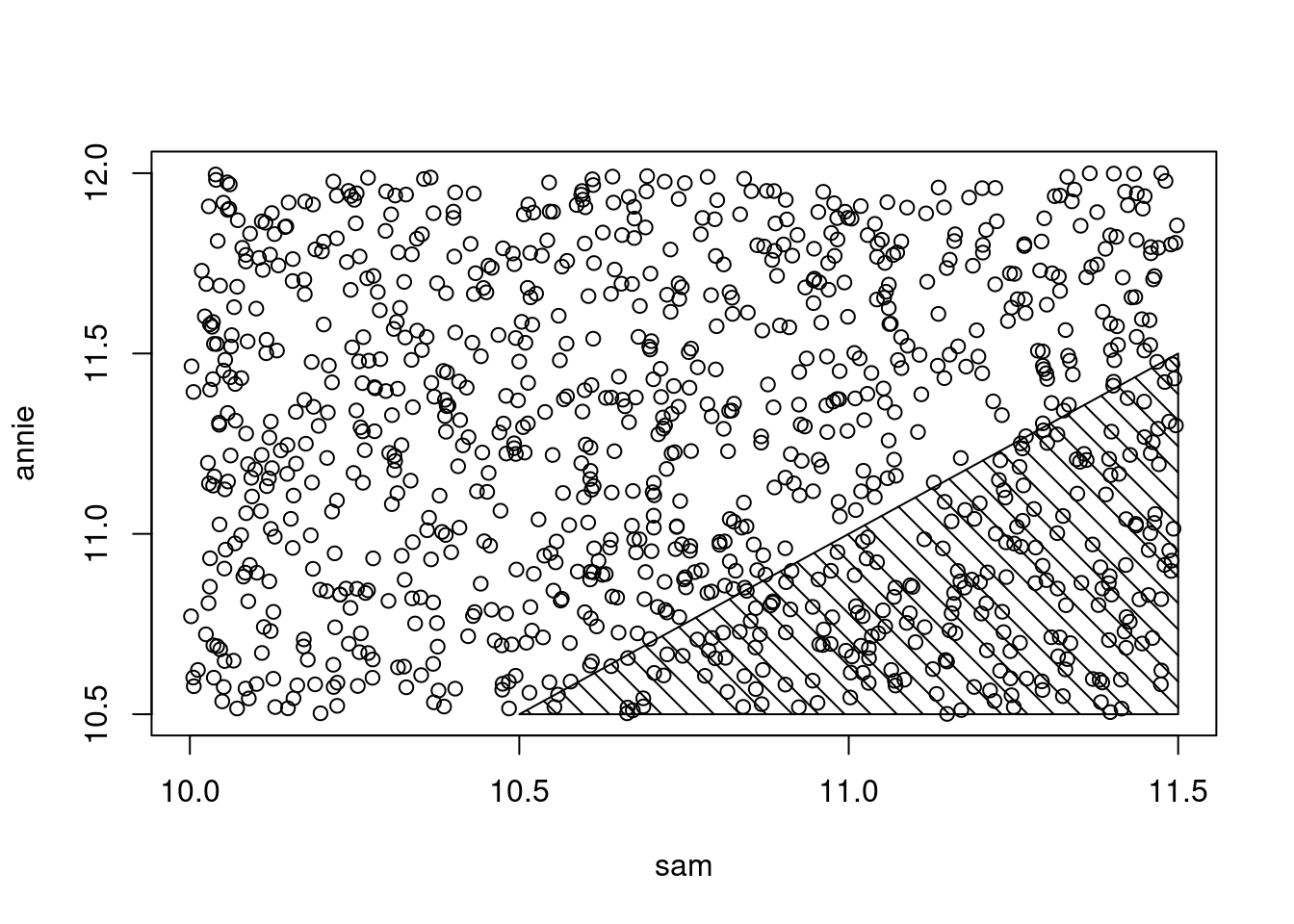
sam = runif(1000, 10, 11.5)
annie = runif(1000, 10.5, 12)We want the probability \(P(A < S)\) which is estimated by the proportion of simulated pairs \((a,s)\) where \(a\) is smaller than \(s\)
prob = sum(annie < sam) / 1000
prob## [1] 0.223The estimated probability that Annie arrives before Sam is 0.223, and the standard error of this estimation is:
sqrt(prob * (1 - prob) / 1000)## [1] 0.01316324In the next plot we can see that the shaded region shows the area in which \(A < S\)
Now, what is the expected difference in the arrival times? Annie is more likely to arrive later, so we model \(E(A-S)\)
difference = annie - samNow we can estimate the mean of the differences using Monte Carlo methods
estimatedMean = mean(difference)
estimatedMean## [1] 0.5079882The estimated standard error is the standard desviation of the difference divided by the square root of the simulation sample size:
SE = sd(difference) / sqrt(1000)
c("Mean" = estimatedMean, "Standard Error" = SE)## Mean Standard Error
## 0.50798819 0.01972754So we estimate that Annie will arrive 0.508 hours after Sam arrives. Since standard error is only 0.02 hours, we can be 95% confident that the true difference is between 0.528 and 0.488 hours